Como indicamos na Parte 1, ligada ao conceito do projeto de timonerias de freio, iremos neste post apresentar um exemplo de cálculo para a definição de uma timoneria hipotética mas que irá valer para a definição de toda e qualquer instalação deste tipo no sistema de freio dos vagões. Desta forma, seguiremos os passos indicados, elegendo um vagão do tipo fechado de mesma série do mostrado em nossa Figura 1, abaixo:

Figura 1 – Vagão Fechado Convencional tipo FRS
Seguindo então a mesma linha de análise descrita anteriormente, verificamos que este vagão fechado possui uma área útil disponível sob o estrado livre de interferências ou sistemas que venham a complicar o projeto de nossa timoneria de freio. Assim, seguiremos usando o espaço entre truques, sempre lembrando que uma timoneria muda de posição pela movimentação das alavancas e tirantes, devido ao desgaste das sapatas e a consequente atuação do ajustador automático de folgas. Para este e demais passos descritos na sequência, recomendo leitura cuidadosa dos itens mostrados na Parte 1 deste trabalho.
O próximo passo é checar o tipo de truques que será instalado no vagão e qual a definição de suas alavancas, se verticais ou se inclinadas. Consultando nossa ferrovia hipotética, vamos supor que o sistema escolhido como padrão seja o de alavancas inclinadas, o que nos dará duas dimensões de alavancas no truque, o que significa uma dimensão maior para a alavanca viva e outra menor para a alavanca morta, presa ao setor de graduação.
Agora vemos que a complexidade de nossa timoneria não deverá ser grande pois como vimos estamos trabalhando com um vagão fechado em sua área entre truques. Desta forma, vamos iniciar considerando apenas duas (2) alavancas principais, as quais estarão conectadas às alavancas vivas dos truques para dar o necessário prosseguimento à força de frenagem para parar nosso vagão quando de uma aplicação de freio feita pelo maquinista. Lembramos aqui, que para efeito de cálculo de definição, consideramos o valor de 2.280 kgf de força feita pelo cilindro 10″ x 12″, quando de uma aplicação de serviço completa.
Os pesos que serão por nós considerados serão: Tara de 28.000 kg e Peso Bruto Máximo de 100.000 kg.
Estes valores serão usados para sabermos se as taxas de frenagem indicadas em norma serão atendidas pelo sistema de nossa ferrovia, a qual também utiliza sapatas fenólicas com coeficiente de atrito de 0,33, operando em uma região de perfil longitudinal predominantemente plano e com trens mistos de até 120 vagões.
Para nossa instalação, iremos aplicar o ajustador automático de folgas entre as duas alavancas principais, local onde ele poderá oferecer o máximo de rendimento por aplicação. Iremos também definir sua aplicação e de seus complementos como a alavanca de comando e a sua posição inicial de montagem.
Definidos estes parâmetros, vamos então visualizar na Figura 2, o esquema inicial de nossa timoneria:
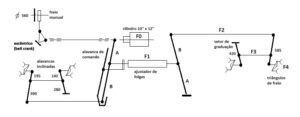
Figura 2 – Esquema da timoneria de freio
Tendo a visão do esquema, podemos iniciar nossa verificação, lembrando que precisamos estabelecer como partida qual seria o valor de taxa de frenagem seguro. Como foi visto na Parte 1 destas notas, as taxas normatizadas estão nas faixas de 15% a 32% da tara do vagão e entre 11% e 14% de seu peso bruto máximo. Desta forma, vamos definir o limite superior da faixa em carregado, ou seja 14% do PBM já que mais à frente nos nossos cálculos teremos que aplicar perdas normais ao sistema, fazendo com que este valor caia.
Tc = 14% = 0,14
0,14 = Fc x 100.000, logo Fc = 14.000 kgf
Esta é a força máxima que nosso sistema fará sobre todas as 8 rodas somadas, para reduzir a velocidade ou parar o trem onde nosso vagão esteja. Vamos checar como ficará a taxa em vazio considerando o máximo de frenagem
Tv = 14.000 / 28.000
Tv = 0,500 = 50% da tara
Este valor não pode ser aplicado pois ultrapassará muito o limite superior de norma que é 32%. Isto nos obrigará a usar no conjunto pneumático um dispositivo vazio-carregado, com 50% de variação, ou seja,
Fv = 14.000 x 0,5 = 7.000 kgt
Tv = 7.000 / 28.000
Tv = 0,25 = 25% da tara. Este valor atenderá nossa necessidade, nos deixando no meio da faixa em vazio.
Resumindo, teremos como base:
Taxa em carregado: Tc = 14% do PBM
Taxa em vazio: Tv = 25% da tara do vagão
Força em carregado: Fc = 14.000 kgf
Força em vazio: Fv = 7.000 kgf
Dispositivo vazio-carregado de variação 50%
Importante: Lembro que estamos usando o “car-set” padrão de freio pneumático composto de cilindro 10″ x 12″, reservatório serviço auxiliar de 41 x 57 litros e válvula tipo ABDX.
Vamos agora definir e calcular a furação das alavancas principais do sistema, que são aquelas ligadas ao cilindro de freio, sua alavanca oposta e a alavanca de comando do ajustador, passando pela análise do sistema de freio manual usado nas operações de estacionamento dos vagões nos pátios.
Como já citamos, o cálculo do sistema de alavancas é bem simples e deve ser iniciado pela força F0, que é aquela feita pelo cilindro de freio para uma aplicação de parada do trem. Vamos então definir as forças que passam pelos tirantes de freio e que puxam as alavancas nos seus pontos de conexão, multiplicando a força inicial em função da furação existente.
Assim,
F0 x (A + B) = F1 x B …. F1 = F0 x (A + B) / B
F1 x A = F2 x (A + B) …. F2 = F1 x A / (A + B) …. F2 = F0 x A / B
F2 x (390 + 195) = F3 x 195 …. F3 = F2 x (390 + 195) / 195 …. F3 = F2 x 585 / 195… F3 = F2 x 3
F3 x 280 = F4 x (140 + 280) …. F4 = F3 x 280 / 420 …. F4 = F3 x 3 x 0,66 …. F4 = F3 x 2
Vamos sempre lembrar que o valor de F4 é o total calculado que chegará a 1 dos triângulos de freio.
Para obtermos a força total será necessário fazer F4 x 4 triângulos. Este valor será o total de força bruta de frenagem.
Colocando então nossa equação de forma sequencial, teremos que Ft será
Ft = F0 x A / B x 3 x 2 x 4 triângulos
Esta é a força total derivada dos cálculos acima, onde ainda temos a indefinição dos valores de A e B, na furação a ser aplicada às alavancas principais. Para descobrirmos os valores de A e B, precisamos seguir um pouco mais à frente em nossos cálculos, encontrando o valor a ser usado como força inicial feita pelo cilindro de freio (F0). vamos, então calcular F0.
Como o cilindro é o ponto de partida da movimentação das alavancas, ele exerce uma força que é provocada pela pressão de equalização quando o maquinista efetua a redução de aplicação e a pressão se estabiliza em 64 psi (0,045 kgf/mm²). Esta pressão aplicada sobre a superfície interna do cilindro, onde se encontra montado um copo de borracha, empurra o êmbolo interno do cilindro para frente, estando este ligado a uma haste metálica presa à alavanca principal do sistema.
Vamos então calcular esta força provocada pela pressão interna no cilindro
P = F / A como
A = ¶ x d² / 4 então, como o cilindro tem 10″ (254mm) de diâmetro, teremos A = ¶ x (254)² / 4
A = 3,1415 x (254)² / 4 nos dá A = 50.670,74 mm² (área interna do cilindro onde o ar comprimido atua)
Para conhecermos a força feita pelo cilindro, aplicamos na fórmula geral e encontramos
P = F / A …. F = 0,045 x 50.670,74 …. F = 2.280 kgf
Este é o valor de força máxima realizado pelo cilindro quando de uma aplicação de serviço total e a usaremos na continuidade do nosso estudo.
Vamos agora continuar buscando os valores de furação A e B das alavancas, transferindo o valor de força no cilindro para a equação abaixo
Ft = F0 x A / B x 3 x 2 x 4 triângulos
Ft = 2.280 x A / B x 3 x 2 x 4 triângulos
Ft = A / B x 54.720 …. 14.000 = A / B x 54.720 …. A / B = 0,256
Sabendo então que o comprimento total das alavancas foi definido como 900mm em função da área disponível sob o estrado do vagão, podemos montar nosso sistema e achar os valores da furação.
A + B = 900
A / B = 0,256 …. desta forma, substituindo encontraremos
A = 0,256 B …. 0,256 B + B = 900 …. 1,256B = 900 ….B = 900 / 1,256 …. B = 716mm
Como A + B = 900 e B = 716, o valor de A será a diferença, ou seja,
A + B = 900 …. A + 716 = 900 …. A = 184mm
Nota Importante: Estes são os valores calculados em função das bases que estabelecemos no início do nosso trabalho. No projeto definitivo, precisaremos manter o ajustador sempre alinhado para que ele não sofra desgastes em suas partes internas e com isso perca a efetividade.
Agora, considerando uma perda de cerca de 30% no sistema, em função das folgas existentes nas conexões, teremos uma ideia mais próxima do que realmente ocorrerá. Vamos então incluir esta perda e ver o que irá acontecer com os valores que acabamos de calcular.
Ft = F0 x R x µ onde
F0 é a já conhecida força feita pelo cilindro, R é a multiplicação proveniente das alavancas do estrado e truque, e µ é o rendimento afetado pela perda de 30%, ou seja, consideraremos uma efetividade de 70%.
Então, teremos
Ft = 2.280 x 184 / 716 x 24 x 0,7
Ft = 9.843,48 kgf
Com esta força mais baixa em função das perdas, teremos as seguintes taxas de frenagem,
Tc = 9.843,48 / 100.000 …. Tc = 0,0984 …. Tc = 9,48% < 11% (valor mínimo da faixa em carregado)
Vejam que considerando a perda de 30% no sistema, o valor total da força de frenagem cairá e com isso teremos um valor de taxa de frenagem abaixo do mínimo da norma. Isso por norma não poderá ser aplicado!
O QUE FAZER ENTÃO??
Como não sabemos se na prática os 30% de perda serão confirmados, vamos modificar o valor de furação das alavancas para compensar parte deste efeito. Vamos aumentar o valor da furação intermediária da alavanca principal de 184mm para 210mm, e acompanhar o que ocorrerá com os cálculos.
Aumentando o valor da furação para 210mm, o outro valor será reduzido pois o comprimento total da alavanca de 900mm não será alterado.
Então, 900 – 210 = 690mm, que será o outro novo valor de furação.
Colocando estes valores nos cálculos, encontraremos
Ft = 2.280 x 210 / 690 x 24 x 0,7
Ft = 11.657,74 kgf
Este novo valor de força total corrigido, nos colocará novamente dentro da faixa de taxa de frenagem em carregado, que é a nossa preocupação em termos de segurança operacional.
Tc = 11.657, 74 / 100.000 … Tc = 0,1165 …. Tc = 11,65% do PBM ….OK
Checando a nova taxa em vazio com a aplicação do vazio-carregado de 50%, teremos
Fv = 11.657,74 x 0,50 …. Fv = 5.828,87 kgf
Tv = 5.828, 87 / 28.000 …. Tv = 0,2081 …. Tv = 20,81% da tara ….OK
Mas, antes de continuarmos, ficam aqui perguntas importantes: Não precisamos checar o que ocorre quando o vagão estiver parado em um pátio e o freio manual for aplicado? Não existe um valor de taxa de frenagem para o freio manual? A resposta é SIM para ambas!!!
Precisamos checar também o freio manual de acordo com sua configuração mostrada no esquema geral da timoneria da Figura 2.
Como a condição mais desfavorável para um vagão parado em um pátio é não deixar que ele se movimente quando estiver carregado, a norma pede que se considere apenas esta condição para um valor mínimo de 10% do PBM. Assim, a força que o freio manual executa sobre as alavancas, precisa chegar às rodas com um esforço que atenda a esta condição. Vamos fazer isso!!
Na Figura 3, segregamos a parte da timoneria do freio manual e sua conexão com o sistema de alavancas que foi objeto do nosso cálculo anterior.
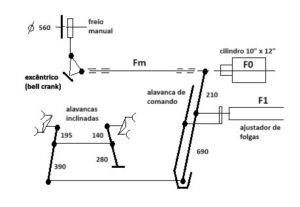
Figura 3 – Timoneria do freio manual
Vamos estudar como a aplicação de força é executada para segurar o vagão no pátio, começando pela caixa de freio manual. Ela possui um volante metálico de 560mm de diâmetro e dentro dela é montado um jogo de engrenagens que visa aumentar a força que um homem normal executa. Pelos valores medidos ao longo do tempo e tendo em vista que a força aplicada pode variar conforme a condição física do operador, ficou definida para efeito de cálculo uma força média de 56 kgf sendo esta força aplicada no aro do volante do freio manual.
Como dissemos, a relação de engrenagens internas da caixa provoca uma multiplicação sendo o valor da relação para a classe de aparelhos padronizada pelas ferrovias brasileiras estabelecido para os fabricantes em 5,36, ou seja, o valor da força aplicada ao lolante já é aumentado em mais de 5 vezes sómente pelas engrenagens internas.
Seguindo a linha partindo da caixa, chegamos ao excêntrico, também conhecido em algumas ferrovias como balancim ou bell crank (USA). Esta peça fundida não é obrigatória nas instalações de freio manual mas algumas vezes recomenda-se sua aplicação quando se precisa incrementar ainda mais o valor da força de frenagem de estacionamento. O excêntrico de freio por sua forma e relação de furação aumenta em mais 32% a força gerada pelo operador e amplificada pelas engrenagens internas.
Como informações necessárias para se fechar o valor da força Fm feita pelo tirante que vem da caixa e passa pelo escêntrico, lembramos aqui que ela é afetada diretamente pela perda devida ao enrolamento da corrente dentro da caixa, o que nos tira produtividade. Este valor do enrolamento máximo definido em norma é de 44,45mm.
Vamos agora escrever a equação de definição de força Fm, necessária a manter um vagão carregado totalmente imóvel mesmo estando carregado no seu limite máximo,
Fm = 56 x 280 (raio do volante) x r x C / D onde
Raio do volante = 280mm
Engrenagens r = 5,36
Excêntrico C = 1,32
Enrolamento D = 44,45
Fm = 56 x 280 x 5,36 x 1,32 / 44,45
Fm = 2.495,8 kgf
Obs: Note-se que esta força é ligeiramente superior aquela proveniente da pressão de equalização no cilindro de freio.
Aplicando-se agora a força Fm no sistema de alavancas do estrado e dos truques, já que o tirante que vem do excêntrico também está conectado com a alavanca principal do cilindro, encontraremos a força provocada pelo freio manual nas 8 sapatas
Fm = 2.495 x (210 / 690) x 24 x 0,7
Fm = 12.757,04 kgf
Isto nos dará uma taxa de frenagem em manual de
Tm = 12757 / 100.000 …. Tm = 12,75% do PBM …. OK
Concluímos então que até este ponto nossa timoneria de freio está atendendo a todos os pontos da norma. Resumimos abaixo os três valores de taxa de frenagem calculados
Vagão carregado: Tc = 11,65% (11% a 14% do PBM)
Vagão vazio: Tv = 20,81% (15% a 32% da tara)
Freio manual: Tm = 12,75% (>10% do PBM)
Atendidos os valores de taxa de frenagem, precisamos agora definir o projeto da alavanca de comando para que o ajustador de folga trabalhe adequadamente, mantendo o curso do cilindro de freio e a distância entre sapatas e rodas.
Este caminho é necessário para que possamos partir para a Parte 3 das nossas notas sobre projeto de timonerias de freio, a qual será dedicada ao dimensionamento dos componentes como alavancas, tirantes, pinos, etc.
Vamos então iniciar, analisando a Figura 4, indicativa da montagem do ajustador de folgas e sua alavanca de comando. Esta figura mostra a montagem em corte frontal para facilitar nosso trabalho de definição dimensional.
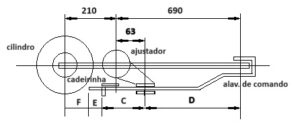
Figura 4 – Esquema da alavanca de comando do ajustador
Para que o ajustador tenha efetividade de trabalho, teremos obrigatoriamente que seguir a relação de proporcionalidade 210 / 690 = C / D. Isto siginifica que a alavanca comandará o giro do corpo do ajustador sob a mesma proporção de furação existente na alavanca principal do sistema. Sem esta proporcionalidade, o ajustador trabalhará fora de sintonia com o desgaste das sapatas, demorando ou acelerando o giro do corpo do ajustador, desbalanceando o movimento de aproximação das sapatas nas rodas e alterando o valor do curso do cilindro para valores maiores ou menores, causando perda ou excesso de força disponível quando uma redução de aplicação de freio for realizada. Em resumo, um grande problema!!
Montando então a relação, podemos ter
210 / 690 = C / D …. como D = 690 – 63 (dist. centro da biela do ajustador) = 627mm
210 / 690 = C / 627 …. logo C = 210 x 627 = C x 690 …. C = 190,8mm = 191mm
Nesta condição teremos então: 210 / 690 = 191 / 627 = 0,304 Plenamente satisfatória!
Lembretes importantes:
A- O valor da cota C define a distância da biela de acionamento do ajustador até o suporte de encaixe que recebe a extremidade da alavanca de comando. Este suporte é conhecido como “cadeirinha” em função de sua forma;
B- A cota E é a distância que deve ser deixada na extremidade da alavanca de comando para que ela não saia da abertura da cadeirinha. O valor mínimo de norma desta cota E deve ser de 76mm (3″) e caso haja a necessidade desta ser menor que este valor normatizado, recomenda-se a aplicação de um pino de retenção.
C- A cota F é a distância da extremidade da alavanca de comando até a linha de centro do cilindro de freio. O valor mínimo para que não ocorra choque do êmbolo interno do cilindro quando de uma aplicação com a ponta da alavanca de comando é de 38mm (1.1/2″).
Checando a alavanca de comando após conhecidos os valores mínimos das cotas E e F, encontraremos
627 + 191 + E + F = 900
627 + 191 + 76 + F = 900 …. estamos inicialmente mantendo aqui os 76mm de extremidade recomendados pela norma para ver o que ocorre com o valor da cota F que precisa ser de 38mm no mínimo.
894 = F = 900 …. F = 6mm …. valor menor que 38mm e portanto não aceitável, nos obrigando a reduzir o comprimento da extremidade da alavanca de comando e instalando um pino de retenção.
Assim, vamos calcular este valor partindo agora do valor mínimo de 38mm da distância entre a ponta da alavanca de comando e a linha de centro do cilindro para ver quanto sobra de extremidade da alavanca de comando,
627 + 191 + E + 38 = 900
E + 856 = 900 …. E = 44mm < 76mm …. teremos que instalar um pino na ponta da alavanca de comando para que ela não desencaixe da abertura na cadeirinha, devido às vibrações que atingem os vagões em serviço.
Temos agora condições de fechar o esquema geral da timoneria de freio do nosso vagão fechado hipotético e resumí-lo na Figura 5, a seguir:
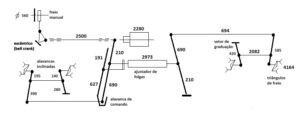
Figura 5 – Esquema dimensional final da timoneria
Agora, como conclusão desta Parte 2 sobre o projeto de timonerias de freio, nos falta verificar a condiição de parada do vagão fechado, sempre com suas rodas girando para evitarmos travamento, o qual poderá ocasionar um calo na superfície de rolamento das rodas, o que será extremamente danoso para o sistema pelos impactos provenientes na via, a cada giro das rodas.
Na Figura 6, abaixo, vemos a condição para que as rodas parem girando quando de uma aplicação
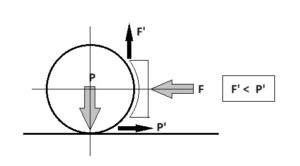
Figura 6 – Condição de frenagem sem travamento
A correta condição de frenagem sem travamento das rodas ocorre quando a força de frenagem F é menor que a força P, representativa do peso do vagão. Como estamos estudando o efeito por roda, vamos calcular 1/8 do que acontece quando o freio a ar for aplicado, levando em consideração o peso do vagão VAZIO, que é a pior situação operacional que favorece o travamento.
As forças indicadas como F’ e P’ são as normais ao sistema e variam com os respectivos coeficientes de atrito entre os materiais. A força F’ varia com o coeficiente sapata x roda e a força P’ com o coeficiente roda x trilho.
F = 1/8 x 5.828 (força de frenagem em vazio) …. F = 728,5 kgf
A componente F’ derivada desta força será
F’ = 728,5 x 0,33 (coef. sapata x roda) …. F’ = 240,4 kgf / roda
Agora, vejamos como calcular o peso P’, seguindo a mesma metodologia de raciocínio
P = 1/8 x 28.000 ….P = 3500 kgf
A componente P’ então será obtida
P’ = 3.500 x 0,10 (coef. roda x trilho) …. P’ = 350 kgf / roda
Vemos que a condição para que não ocorra o travamento foi plenamente atendida, ou seja,
F’ < P’ …. 240 kgf < 350 kgf As rodas não irão travar durante as aplicações de freio
Com esta verificação fechamos este estudo, deixando agora como Parte 3 do projeto de timonerias, a etapa que trata do dimensionamento das peças do sistema como alavancas, tirantes, pinos, garfos, etc.
Até breve!!