1- O CONCEITO DA RELAÇÃO PESO X ALTURA
Todos nós sabemos que os vagões ferroviários possuem estruturas que são projetadas para o transporte seguro dos mais diferentes tipos de produtos. Tal projeto pode contemplar vagões abertos ou fechados, em função da necessária proteção contra as intempéries, bem como dimensões específicas às condições de carga e descarga nos terminais. Além disso, tais dimensões podem também estar condicionadas à densidade dos produtos quando a carga for transportada sob a forma de granel sólido ou líquido, como cimento e combustíveis.
A estrutura com seu correspondente volume, irá gerar uma lotação (carga) que somada à tara do vagão (seu peso vazio), irá resultar no seu peso bruto máximo sobre trilhos (PBM). Este PBM é descarregado na via permanente pelas rodas dos truques, existindo portanto oito (8) pontos de apoio nos trilhos. Porém, precisamos lembrar que pelas rodas não passam apenas as cargas verticais (V) referentes ao peso. Nelas também atuam as forças laterais (L) devidas à dinâmica orientada pela superfície em ângulo das pistas de rolamento. Como já citamos várias vezes, as rodas ferroviárias não são cilindricas mas sim, cônicas.
Durante todo o tempo que o vagão estiver circulando, o conjunto de forças verticias (V) e laterais (L) estará atuando sobre as rodas, criando uma relação fundamental conhecida como relação L / V. Esta relação analisa o que ocorre no contato da roda com o trilho para a checagem da estabilidade em operação, sendo de extrema importância que para que o vagão circule com segurança, a relação L / V seja menor que 1. Assim,
L / V < 1, significa que a circulação está segura pois as cargas verticais (V) são maiores que as carga laterais (L).
L / V = 1, significa que estamos no limiar de um descarrilamento pois as cargas laterais (L) se igualam às cargas verticais (V).
L / V > 1, significa que ocorrerá ou já ocorreu um descarrilamento pois as cargas laterais (L) ficaram maiores que as cargas (V), fazendo com as rodas escalem os trilhos.
Destacamos esta relação pois a verificação da resultante das forças que atuam sobre as rodas tem sua origem na posição do Centro de Gravidade (CG) do vagão. A oscilação da caixa em função da velocidade, a posição da carga no interior do vagão, as distorções da via permanente e até a força de vento atuam sobre o CG, o qual afeta diretamente a relação L / V, sendo portanto muito importante que antes de iniciarmos uma verificação de estabilidade, tenhamos conhecimento da posição do Centro de Gravidade, ou seja o CG do vagão. Todas as referências de todas as forças que tendem a tombar o vagão ou a equilibrá-lo, passam pelo seu CG e por isso é muito importante entender como localizá-lo. Vemos na Figura 1 abaixo, o esquema de forças atuantes entre rodas e boletos dos trilhos, retirada do capítulo 8 do livro “Estradas de Ferro” Volume 1 – Helvécio Lapertosa Brina. Esta imagem nos mostra um vagão em uma superelevação “h”, que é a diferença de altura entre o trilho externo e o trilho interno. Esta mesma condição de diferença de altura constrói o ângulo “∝” usado na decomposição de forças quando viermos a falar aqui de verificações mais rápidas de estabilidade.
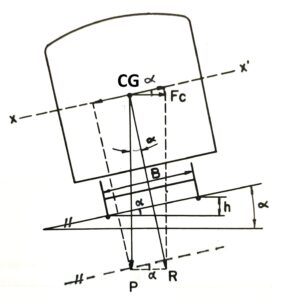
Fig. 1 – Esquema de forças quando de circulação em superelevação
Não vamos correr o risco de falar demais em estabilidade neste momento, sem primeiramente apresentar uma forma básica e simples de cálculo do centro de gravidade de um vagão ferroviário. Por isso, vamos destacar algumas ideias importantes:
1- Como nossa referência básica é a via permanente, a altura do CG deve estar sempre relacionada aos trilhos. Esta é nossa regra “áurea”, já que lá é o lugar onde tudo acontece quando o trem está em movimento;
2- Cada item que compôe o vagão tem um determinado peso, que somado aos pesos dos demais componentes, formam o peso final do vagão;
3- Cada um dos pesos de cada componente, deve também ter sua referência de altura em relação aos trilhos;
4- A carga útil do vagão (lotação) também deve estar referenciada aos trilhos, já que como dissemos todos os pesos somados passam pelas rodas;
5- Importante lembrarmos que a altura de cada componente em relação aos trilhos irá variar em função do recalque (abaixamento) do pacote de molas. Exceção nesta variação de altura deve ser feita aos fundidos das laterais dos truques e aos rodeiros, os quais não sofrem tal variação;
6- Vagões dos tipos gôndola e plataforma podem ter seus CGs afetados em função de coroamento, no caso dos minérios, ou dimensões da carga;
2- O EFEITO DA SUSPENSÃO DOS TRUQUES
Temos total consciência de que os modernos softwares de cálculo estrutural, os quais atuam diretamente sobre modelos 3D, mostram de forma automática a posição do CG para a caixa, truques, engates, freio, lotação, etc. No entanto, de nada adianta utilizar um software se o usuário não souber a teoria que gerou sua concepção. O Engenheiro não pode acreditar no que o computador lhe apresenta sem ter uma avaliação crítica se aquilo que está sendo respondido é coerente, ou não. Como disse, esta é a minha visão com respeito à automatização da maioria dos cálculos que usamos em Engenharia Ferroviária. Respeito a posição contrária, caso o amigo leitor não entenda desta forma!!
Vamos então iniciar uma forma mais direta de calcular a altura do CG de um vagão ferroviário. Muito importante esclarecer que quando calculamos os vários valores de peso x altura de cada componente e da carga embarcada no vagão em relação aos trilhos, estaremos estabelecido um certo tipo de média ponderada, ou seja, quanto maior for nosso detalhamento em termos da quantidade de componentes em função de sua altura aos trilhos, mais preciso será o valor geral do CG.
Uma observação fundamental é que se conheça bem o tipo de suspensão e a quantidade de molas helicoidais aplicada em cada pacote no truque, ou seja, as molas internas e as molas externas que os compôem. O ambiente de nossas ferrovias, classifica as molas helicoidais ferroviárias por códigos. Elas variam da codificação tipo D2, que representa as molas de maior rigidez, mais baixas e resistentes ao abaixamento, até a codificação D7 que são as mais altas e flexíveis.
Também é importante lembrar que a forma de cálculo que apresentaremos em função do abaixamento da suspensão, não levará em consideração o efeito das molas das cunhas de fricção. Para nossa ideia de posição do CG, esta precisão não será necessária. As cunhas podem dificultar o abaixamento em função do atrito gerado pela normal à força de contato destas com as chapas das colunas das laterais dos truques e caso o leitor queira aprimorar seu cálculo, poderá incluir as molas das cunhas e suas respectivas constantes.
Veja na tabela a seguir os tipos de molas ferroviárias usadas em vagões e sua respectiva rigidez.
| MOLA | POSIÇÃO | RIGIDEZ (kgf/mm) |
| D2 | externa | 175,40 |
| interna | 59,20 | |
| D3 | externa | 76,60 |
| interna | 30,70 | |
| D4 | externa | 53,20 |
| interna | 20,00 | |
| D5 | externa | 40,00 |
| interna | 20,00 | |
| D6 | interna | 24,90 |
| D6A | interna | 8,30 |
| D7 | externa | 36,30 |
| interna | 17,50 |
Olhando para esta tabela, observamos que quanto menor o número de referência, maior será sua rigidez. Isto significa que as molas D2 são muito mais “duras” que as molas D7, que são bem mais flexíveis. O amigo que nos acompanha, poderia perguntar porque as molas são assim classificadas e eu responderia que tudo depende da dinâmica dos vagões em circulação e o cálculo de suas frequências. Pode ser necessário o uso de uma suspensão mais resistente para manter estável a relação de frequência de um determinado vagão em relação às características da via permanente do trecho onde ele for circular. Sobre esta questão de frequência na dinâmica ferroviária, voltaremos ao tema em um post específico que faremos no futuro.
Também lembramos que as molas ferroviárias são montadas umas dentro das outras para que suas rigidezes sejam somadas na resistência ao abaixamento. Por isso, indicamos em cada pacote a quantidade de molas externas e a quantidade de molas internas, sendo possível que em determinada posição, não sejam aplicadas molas internas, enquanto que em outro projeto sejam aplicadas molas adicionais como as D6A, que são molas internas de menor dimensão aplicadas dentro das molas internas regulares, para gerar um aumento de reserva dinâmica contra a condição de “molas sólidas” que ocorre quando a mola fecha todas as suas espiras. Esta condição deve ser evitada a qualquer custo pois o impacto produzido pode gerar quebras nas próprias molas assim como danos nos rolamentos, rodas, fundidos, partes da estrutura do vagão, bem como nos componentes da via permanente como dormentes, fixação, placas de apoio, nas cabeceiras e estruturas das pontes e por aí vai…
3- O CÁLCULO DO CENTRO DE GRAVIDADE
Vamos então escolher um vagão para demonstrar a maneira deste cálculo que mostra a posição estimada do Centro de Gravidade.
Decidimos por um vagão hopper graneleiro de grande capacidade, bitola 1,60m e projeto inteiramente dentro das indicações das normas NBR e AAR, conforme mostrado na Figura 2, abaixo:

Fig. 2 – Vagão graneleiro HFT
Vamos agora indicar as caracteristicas de peso e de dimensões que serão usadas em nosso cálculo:
TARA: 31.000 kg / TRUQUES: 10.000 kg / ESTRUTURA: 21.000 kg / LOTAÇÃO: 89.000 kg / PBM: 120.000 kg
O esquema dimensional dos principais componentes e suas respectivas alturas em relação ao topo dos trilhos é mostrado a seguir:
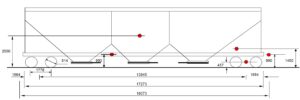
Veja que cada um dos principais conjuntos que compôem o vagão está indicado no esquema dimensional, assim como suas alturas em relação ao boleto dos trilhos que é a nossa referência. Desta forma, destacamos em um ponto vermelho a posição estimada de montagem na estrutura do vagão e sua altura respectiva, sendo usados, A. os truques com seu peso individual aplicado no centro das laterais; B. o sistema de freio acima da linha do estrado; C. o sistema de choque e tração na linha de engates; D. o conjunto do estrado com as longarinas e as tremonhas também com peso individual estimado na linha de engates; E. a caixa estrutural formada pelas paredes laterais, os apoios de rampa, as cabeceiras e a cobertura com suas escotilhas passadiços, etc. Também como destacado anteriormente, ratifico que quanto mais elementos forem considerados pelo calculista, mais preciso será o resultado final. O termo “preciso” significa que mais componentes darão um resultado de altura de CG mais próximo da realidade.
Atenção para o fato de que cada uma das alturas indicadas é considerada no esquema sem o abaixamento dos 4 pacotes de molas dos truques. Para ajustar esta condição, calcularemos o abaixamento tanto na condição de vagão vazio, que significa quanto os pacotes cedem considerando o peso sem a lotação e na condição de vagão carregado, quando a carga for aplicada no terminal. Tal abaixamento, como já dissemos anteriormente, é definido pela quantidade de molas helicoidais usada em cada pacote. No nosso caso, usaremos um truque RIDE CONTROL cujo projeto básico indica nove (9) molas externas D3 e sete (7) molas internas também do tipo D3.
Cada pacote de molas D3 na quantidade indicada, nos dará:
(9 x 76 kgf/mm) + (7 x 30kgf/mm) = 894 kgf/mm
Como temos 4 pacotes de molas de suspensão por vagão:
4 x 894 kgf/mm = 3.576 kgf/mm , valor que será aplicado para calculo dos recalques em vazio e em carregado.
Recalque em vazio: peso da caixa estrutural menos o peso dos truques + o peso das 2 travessas centrais, que estão apoiadas sobre as molas
31.000 kg – 10.000 kg + (2 x 750 kg) / 3.576 kg/mm = 6,29 mm
Recalque em carregado: igual ao cálculo anterior, agora incluindo o peso da lotação
31.000 kg – 10.000 kg + (2 x 750 kg) + 89.000 kg / 3.576 kgf/mm = 31,18 mm
Assim, cada altura de cada componente deverá ser ajustada de acordo com o recalque calculado em cada condição e os valores multiplicados pelo respectivo peso de cada um. Todos estes valores calculados deverão ser somados e divididos pela tara ou pelo peso bruto máximo para acharmos a altura estimada do CG em cada situação.
Vamos ver esta sequência a seguir:
Truques 10.000 kg x 450,71 mm
Engates 1.200 kg x 983,71 mm
Freio 800 kg x 1.443,71 mm
Estrado 7.600 kg x 983,71 mm
Caixa 11.400 kg x 2.493,71 mm Valores somados = 42.746.950 kgf/mm
O Centro de Gravidade do vagão vazio será obtido, dividindo-se este valor total pela tara (T)
CG VAZIO = 42.746.950 kgf / mm / 31.000 kg
CG VAZIO = 1.378,93 mm
Fazendo agora o mesmo raciocínio para a a condição carregado, encontraremos:
Truques 10.000 kg x 425,82 mm
Engates 1.200 kg x 958,82 mm
Freio 800 kg x 1.418,82 mm
Estrado 7.600 kg x 958,82 mm
Caixa 11.400 kg x 2.468,82 mm
Lotação 89.000 kg x 2.468,82 mm Valores somados = 261.711.090 kgf/mm
O Centro de Gravidade do vagão carregado será obtido, dividindo-se este valor total pelo peso bruto máximo (PBM)
CG CARREGADO – 261.711.090 kgf / mm / 120.000 kg
CG CARREGADO = 2.180,92 mm
Podemos então fazer alguns comentários para o fechamento deste post:
• Os valores encontrados estão perfeitamente dentro dos limites citados nas normas brasileiras (NBR) e norte-americanas (AAR).
• O valor do CG carregado calculado, está abaixo do limite de 2.500 mm para vagões da bitola 1,60m. (2.000 mm para a bitola 1,00m).
• Como citamos, quanto mais aprimorada a divisão de componentes, mais precisos serão os valores encontrados em relação ao CG real.
• As alturas limite indicadas nas normas, são fixados em função da relação L / V que mantém a estabilidade do vagão.
• O valor do CG abaixo da metade da altura do vagão se explica por seu projeto, ou seja, as tremonhas ficam cheias de produto abaixo da linha de engates, puxando a média para um valor menor. Este efeito poderia não ser tão significativo no caso por exemplo de um vagão fechado, onde não existe possibilidade de ter peso de produto abaixo da linha de engates.
Peço ao amigo que se interessar em utilizar este artifício de cálculo do CG, que caso tenha dúvidas ao que foi apresentado ou queira entender algum ponto específico, que faça contato pelas vias indicadas. Será um prazer conversar sobre vagões.
Obrigado e até o próximo post.

