Meus caros amigos,
Ao longo de todos estes anos dedicados ao projeto de material rodante ferroviário, sempre tive a oportunidade de encontrar alguns companheiros de prancheta (hoje computador!!), que me perguntavam sobre as forças de atrito geradas nas cunhas de fricção dos truques, responsáveis pela estabilidade dos vagões quando em movimento. Como eles deveriam considerá-las nos projetos? Como calcular um valor que pudesse ser utilizado para entender o fenômeno?
Não são perguntas assim tão fáceis de serem respondidas porque a quantidade de variáveis é bem grande e principalmente para os truques de pressão variável nas cunhas em função da lotação do vagão, acredito que a melhor forma de entender e sentir o problema seria tentar modelá-lo e montar equações diferenciais já que quanto mais o vagão está carregado mais força as cunhas fazem contra as chapas de desgaste das colunas das laterais dos truques, ao mesmo tempo que perdem altura com o recalque das molas.
Mas, não precisamos ficar preocupados e interromper a leitura destas notas pois não pretendo seguir aqui este caminho academico e mais acertivo. Talvez para os estudantes de engenharia, este seria um bom tema para os trabalhos de conclusão de curso mas aqui iremos “parcializar” o raciocínio para um entendimento mais rápido.
Vamos então procurar entender o que ocorre na região das cunhas de fricção pelos pontos a seguir e recomendando a leitura do nosso estudo postado em julho de 2017, quando conversamos sobre os sistemas de amortecimento que existem nos truques:
1- Como sabemos, existem dois sistemas de amortecimento conhecidos para os truques ferroviários de carga: pressão constante e pressão variável com a lotação do vagão;
2- A moderna Engenharia Ferroviária tem se dedicado a estudar o sistema de pressão variável quando a força exercida pelas cunhas de fricção sobre as colunas das laterais vai aumentando à medida que as molas vão recalcando sob a lotação;
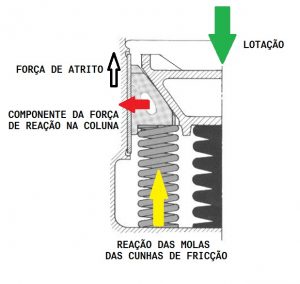
3- Observemos com cuidado a Figura 1, a seguir e veremos este a ação da LOTAÇÃO força o sistema para baixo. As molas ao serem pressionadas reagem com FORÇAS DE REAÇÃO contrárias a este movimento. No caso das cunhas de fricção, suas molas reagem como as demais, gerando uma COMPONENTE DA REAÇÃO, proveniente da decomposição de forças pelo ângulo das cunhas e das rampas da bolsa de montagem nas travessas.
Figura 1 – Esquema de reação das forças nas cunhas de fricção
4- Pela segunda lei do atrito, “A força de atrito é proporcional à ação normal que a superfície exerce sobre o corpo que a pressiona“. Logo, quando do abaixamento das cunhas e o consequente aumento de pressão das cunhas sobre as chapas da lateral, é criada uma força perpendicular e proporcional a esta, que é a Força de Atrito;
5- A Força de Atrito gerada pela cunha sobre a coluna varia com o coeficiente de atrito das duas superficies, no nosso caso aço x aço. Mudando-se este coeficiente, mudar-se-á o valor da força de atrito gerado;
6- O ângulo das cunhas e das rampas nas travessas igualmente regula o valor da reação criada e que pressiona a coluna da lateral. Assim, se também mudarmos este ângulo, mudaremos a reação sobre a coluna.
O que passaremos a discutir a partir deste ponto é como calcular o valor da Força de Atrito em cada uma das cunhas de fricção, porém como dissemos ao iniciarmos este trabalho, de forma resumida pois precisaríamos de um sistema bem mais complexo para avaliar todas as variáveis. Então, nos concentraremos em encontrar o atrito nas colunas, esquecendo propositalmente os demais atritos de contato entre cunha e superfície das rampas, tolerâncias dimensionais das peças, etc.
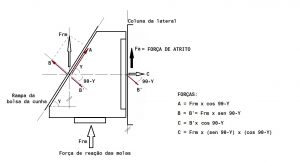
Vamos então estudar a Figura 2, onde as cunhas são separadas para nosso entendimento da decomposição das forças de contato na região:
Figura 2 – Esquema de forças para cálculo da Força de Atrito
Observando-se a Figura 2 e fazendo a decomposição das forças desde a Força de Reação (Frm) proveniente das molas da cunha, vemos que pela teoria dos Eixos Paralelos conseguimos calcular a Força C que é a força horizontal decomposta do contato da cunha com a rampa da bolsa na travessa, sobre a chapa da lateral. Tendo-se calculado esta força, vamos então aplicar a 2a Lei do Atrito e chegar a: Fa = T x C .
O coeficiente de atrito T, como dissemos, varia em função dos materiais e a Força C é calculada pela Figura 2:
C = Frm x (sen 90-Y) x (cos 90-Y), sendo Y o ângulo de projeto da cunha de fricção.
Para o cálculo da Força de Atrito em cada uma das cunhas de fricção, vamos multiplicar o valor encontrado pelo coeficiente de atrito entre as duas superficies:
Fa = T x (Frm x (sen 90-Y) x (cos 90-Y))
Esta é a Força de Atrito calculada a partir apenas das variáveis criadas pelas molas das cunhas, pelo ângulo das cunhas e pelo coeficiente de atrito dos materiais usados no projeto.
Como exemplo prático, em um moderno truque ferroviário usado em vagões hopper graneleiros de 150 m3 de capacidade com tara de 29.000 kgf, a força de atrito calculada em cada uma das cunhas de fricção e contrária ao movimento do abaixamento, pode chegar a 428 kgf somente pela ação de instalarmos a caixa estrutural vazia sobre os truques, ou seja, é a força gerada pela reação de recalque das molas da cunha desde a condição de altura livre até a posição de vagão vazio e pronto para inicio do trabalho.
Esta força será significativamente aumentada quando o vagão for carregado com a lotação para a qual foi calculado, além de proporcionar a estabilidade dinâmica necessária à operação ferroviária quando o vagão estiver nos trens regulares. Como cada vagão tem 8 cunhas de fricção, estas peças juntas, equilibrarão e amortecerão as vibrações que tentem a instabilizar o veículo.
Os projetistas ferroviários de truques, vêm estudando continuamente materiais, geometrias e montagens para controlar cada vez mais os aspectos dinâmicos dos vagões, já que as velocidades operacionais têm aumentado bem como a lotação dos trens. Estudar a Ferrovia é ainda um desafio para os Engenheiros Brasileiros que saem das escolas sem experiência neste campo tão importante.
Abraço Fraterno!!