Uma das grandes dúvidas dos engenheiros ferroviários é o cálculo do raio mínimo de inscrição do material rodante nas curvas da ferrovia. Cada estrada de ferro tem seus perfis longitudinal e vertical derivados de sua implantação nos terrenos de projeto, fazendo com que haja mais ou menos curvas, obras de arte, etc
Desta forma, quando necessitamos especificar locomotivas, vagões ou carros de passageiros, torna-se imprescindível definir suas dimensões limite em função do gabarito e dos raios das curvas. Em resumo, quando calculaos o raio mínimo que um projeto específico possui, o fazemos de fato para comparar com aqueles raios físicos existentes nos trechos concluindo então se nosso veículo poderá circular sem riscos de descarrilamento e para encontrar a dimensão mais adequada e os equipamentos mais indicados para truques e engates.
As formas de cálculo que resumiremos neste e no exemplo do próximo post, são aquelas usadas pelas ferrovias norte-americanas e que são também adotadas no Brasil por similaridade de funcionamento dos trens longos e pesados que utilizamos. Serão considerados aqui somente os raios mínimos das curvas horizontais, os quais provocam o deslocamento dos dois engates acoplados e das estruturas dos vagões em planta, sendo este de fato o motivo do nosso estudo. A norma também prevê o cálculo de raios mínimos verticais mas não os estudaremos por enquanto por serem menos críticos que os horizontais.
De forma geral, sabemos que os modelos de engates para vagões possuem dois tipos básicos de cabeça de acoplamento, E ou F, mas que suas hastes variam em forma e dimensão exatamente para permitir variações nos ângulos laterais nas curvas. O engenheiro ferroviário deve optar pelo modelo mais adequado tecnicamente.
Os espelhos, que são aquelas peças montadas para proteger as extremidades das vigas centrais, seguem a mesma linha dos engates. Podem possuir base de apoio provida ou não de molas e uma abertura compatível com o tipo de haste do engate. Quanto mais longa for a haste do engate, maior a abertura necessária nos espelhos.
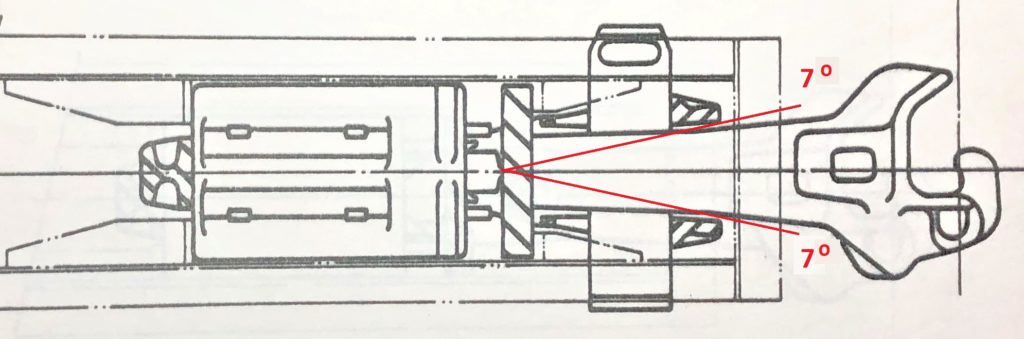
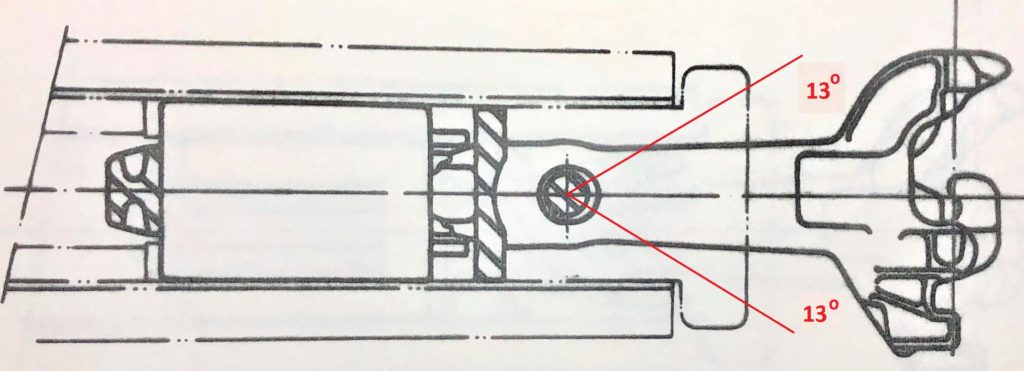
Observando-se as duas figuras acima, vemos o máximo ângulo de giro, o qual provoca um deslocamento lateral quando dois engates acoplados entram nas curvas. Tal deslocamento, para efeito de cálculo, deve ser considerado desde o ponto onde a haste do engate se conecta com a braçadeira, também conhecido como ponto de pivotamento até as faces de tração das mandíbulas que são as partes que mantém os dosi engates acoplados.
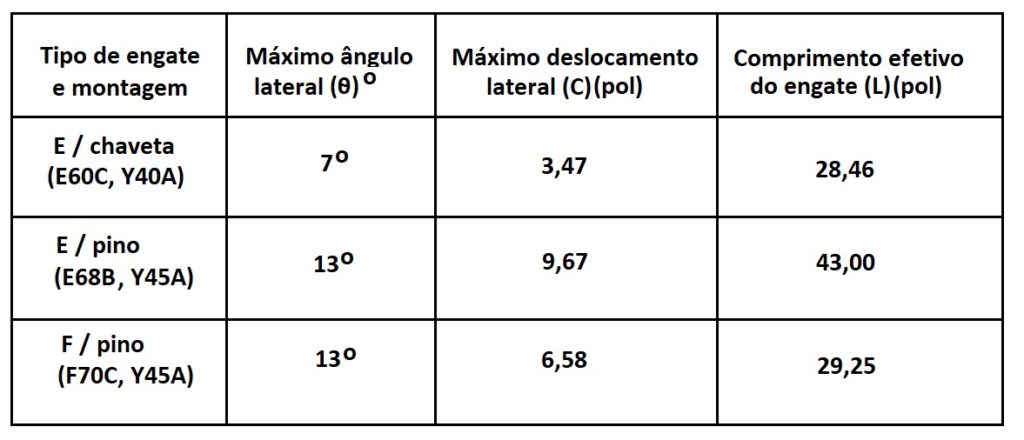
Na Tabela 1, apresentada na sequência, podemos observar os daods básicos de movimentação lateral para os tipos de engate mais usados aqui no Brasil para vagões. Existem outros tipos mas que não serão abordados para que possamos nos concentrar no que realmente será útil a quem quiser utilizar este conceito de cálculo. Para referência na norma AAR, buscar a Seção C-II item 2.1.4.
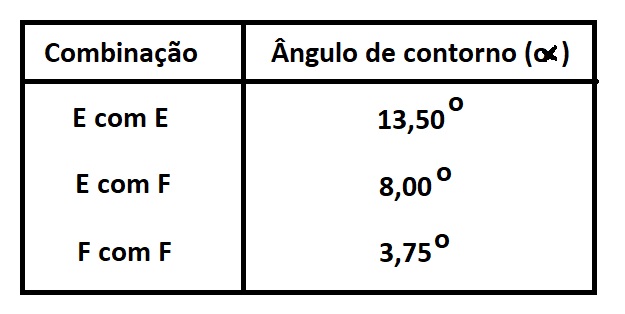
Já na Tabela 2, temos o máximo ângulo de contorno entre as linhas de centro de dois engates acoplados. A combinação entre os tipos de engate provoca diferentes ângulos de contorno em função das características da geometria da cabeça, do comprimento da haste e da fixação do engate na braçadeira, se por meio de chaveta ou pino.
Para complementar nosso entendimento relativo ao uso dos valores das duas tabelas mostradas, o engenheiro deverá ao especificar seu vagão, indicar o melhor tipo de engate em função de alguns parâmetros como:
* Tipo de engate existente na frota, se E ou F;
* Perfil longitudinal de sua via permanente, com indicação dos raios de curva;
* Formação de seu trem tipo ou possibilidade de formação dos trens
* Como será feita a operação dos trens (tração apenas frontal, remota, auxílio de cauda, etc).
Vejamos a família de engates mais usados no Brasil, os quais são referenciados nas tabelas e que serão citados em nosso texto e cálculos:

Engates E60: Cabeça E com cauda para chaveta
Engates SE60: Cabeça E com anti-engavetamento e cauda para pino
Engates E68: Cabeça E com cauda para pino
Engates F70: Cabeça F e cauda para pino
Na inscrição de dois vagões em uma curva horizontal, a definição dada para o tipo de sistema de choque e tração será fundamental pois um sistema agirá em relação ao outro, gerando ângulos laterais correspondentes aos deslocamentos individuais de cada um dos engates.
O critério mais importante a considerar quando dois engates estiverem na inscrição em determinada curva, é aquele que indica que os engates acoplados se deslocarão lateralmente em relação à linha de centro de cada viga central e que ando isto ocorrer suas hastes não encostem nas laterias dos espelhos, já que estes determinam a abertuta limite. Caso haja este contato çateral, o vagão menor e com menor abertura de espelho, além de menor tara, poderá ser pressionado pelo vagão maior e mais pesado para fora da via até que as pistas percam contato com o boleto do trilho e o vagão descarrile.
Como o cálculo do raio mínimo provém da norma AAR (Association os American railroads), ele utiliza fórmulas empíricas provenientes de estudose testes práticos que relacionam a posição dos veículos como se um deles estivesse na via tangente (reta) imediatamente anterior à entrada da curva e o outro como se já na curva estivesse.
Sabendo que o comprimento dos vagões pode variar muito em função do produto que eles transportam, a norma estabelece para facilitar nossa análise, a existência de um “vagão base AAR” provido de engates tipo E (E60) com comprimento de haste e dimensões conhecidas e mostradas a seguir. Combinar o vagão específico que estamos querendo checar e cujo raio mínimo precisa ser calculado, com o “vagão base AAR”, será o nosso trabalho na continuidade e no exemplo prático da continuação no próximo post.
Sempre se deve seguir a dias verificações básicas:
A- Estando o “vagão base” na tangente e o novo projeto na curva;
B- Estando o “vagão base” na curva e o novo projeto na tangente.
Em ambas as condições o ângulo de contorno entre as cabeças deve ser checado para sabermos se é ultrapassado em relação aos valores indicados na Tabela 2 que foi apresentada acima.
São as seguintes as dimensões do “vagão base AAR” para os cálculos:
* Comprimento entre faces de tração dos engates: 13.600mm (44,62 pés)
* Comprimento entre espelhos: 12.800mm (42,00 pés)
* Comprimento entre centros de truques: 9.470mm (31,96 pés)
* Distância do pião à face do espelho (over hang): 1.665mm (5.46 pés)
* Folga entre o engate e o espelho: 95mm (0,31 pés)
Fica então a pergunta: EM QUANTAS E QUAIS SITUAÇÕES TEMOS QUE CHECAR A INSCRIÇÃO PARA ENCONTRAR O VALOR DO RAIO MÍNIMO PARA NOSSO VAGÃO ESPECÍFICO? Vamos então citar estas condições de verificação e tentar entender cada uma delas:
I- Vagão circulando desengatado de trem ou locomotiva-
Esta condição pode parecer incomum mas é usada nas manobras de pátios de gravidade muito usados nos EUA, quando os vagões são soltos em rampa e passam por vários AMVs de via diferentes para a formação simultânea de vários trens. Recomendo assistir vídeos no You Tube que tenham no título o termo em Inglês HUMP YARDS, para melhor visualização desta situação. Então, os raios mínimos desta condição são os seguintes:
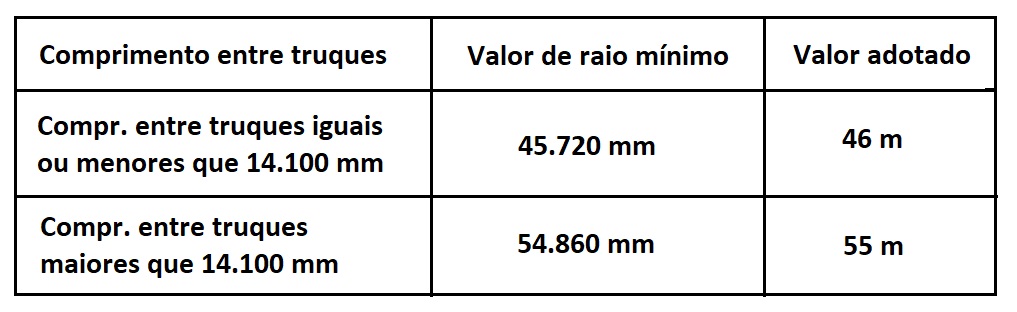
Porém, como os vagões também circulam engatados nos Hump Yards e estes pátios não formam a maioria dos trechos para manobras ou viagens, igualmente necessário se torna checar os ângulos de contorno dos engates do vagão de projeto e do “vagão base” nas duas situações descritas anteriormente, ou seja, em tangente e curva.
II- Vagão engatado a vagão igual e de mesmo projeto –
A norma indica para esta condição os seguintes valores:
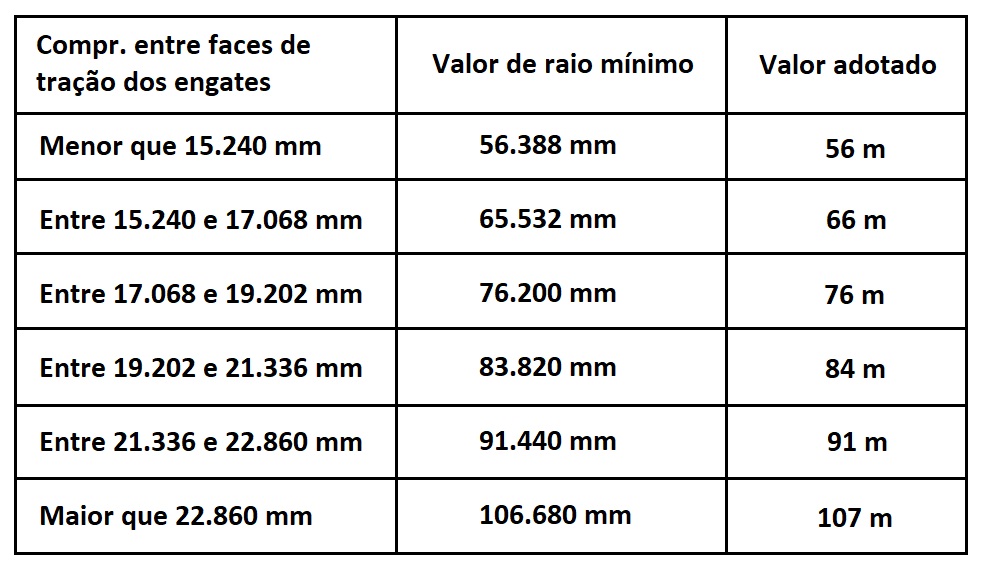
III – Vagão engatado ao “vagão base”, ora em tangente, ora em curva –
Em circulação normal cada valor calculado nestas condições deve ser comparado com os demais valores para se definir o valor oficial do raio mínimo, lembrando que este será aquele que for o maior de todas as verificações.
Vamos então passar a estudar as fórmulas para cálculo de raio mínimo para curvas horizontais, tomando por base alguns preceitos comprovados fisicamente. A condição mais crítica é a inscrição de tangente e curva sem uma compensação de gabarito lateral como aquela encontrada em trechos antigos de nossas ferrovias. Nesta condição, como já mencionamos anteriormente, um dos vagões está na tangente no ponto exato de entrada da curva e o outro, já dentro da curva propriamente dita.
Normalmente o pior caso ocorre quando o vagão mais curto está na tangente, o que não elimina a necessidade de estudar o caso oposto. Assim, dois vagões engatados e ambos equipados com engates tipo F podem apresentar uma condição mais restritiva em termos de ângulo de contorno do que se fossem equipados com engates do tipo E.
Para utilizar as fórmulas de cálculo, os itens com índice (1) devem ser tomados para o vagão que estiver na tangente e os itens com índice (2) para aquele que estiver na curva.
Observemos atentamenteos dois esquemas que se seguem e veremos que os cálculos são baseados em pura geometria e análise angular. O restante é visualizar a movimentação dos vagões para saber se nas condições de inscrição poderá ou não haver um final de giro lateral que possa comprometer a segurança operacional.
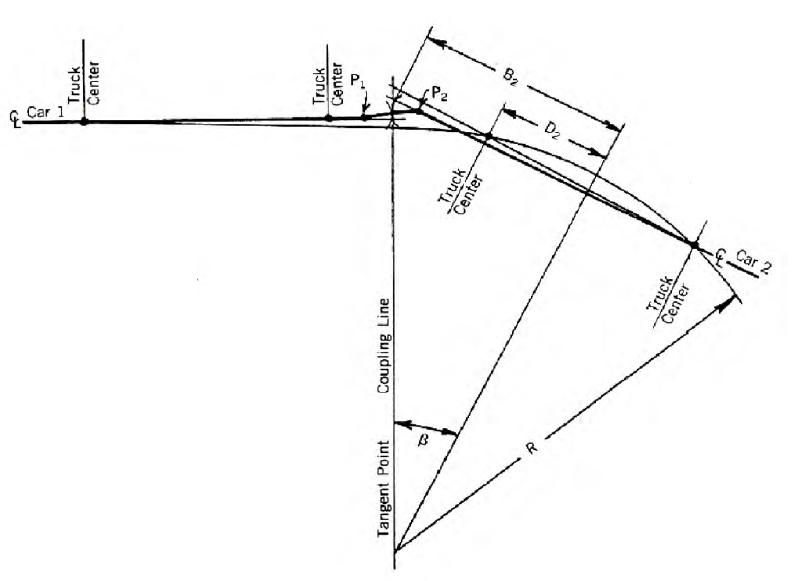
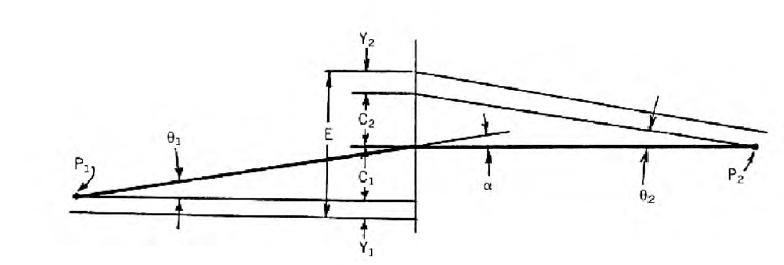
Nestes esquemas, retirados da norma AAR, vemos as dimensões e ângulos que são citados nas fórmulas a seguir sendo que o segundo deles é uma ampliação do que ocorre entre os pontos P1 e P2 do primeiro esquema, ou seja, um facilitador de visualização de limites de hastes, folgas e deslocamentos das duas cabeças de engate acoplada.
SITUAÇÃO 1: Raio mínimo determinado pelo ângulo de contorno ALFA.
Fórmulas:
R = (B2)² – (D2)² – E² / 2E Equação 1
E = Y1 + C1 + Y2 + C2 / 12 Equação 1.1
Y = 0,625 (B / D) + 0,625 Equação 1.2
β = Arcsen (B2 / R + E) Equação 1.3
α = θ1 + β – θ2 Equação 1.4
Onde:
R = Raio mínimo calculado
B = Metade da distância entre as faces de tração dos engatesâ
D = Metade da distãncia entre truques
E = Deslocamento lateral total entre as linhas de centro dos vagões
C = Máximo deslocamento lateral permitido para cada tipo de engate
Y = Deslocamento lateral na linha de centro dos vagões
α = ângulo de contorno horizontal
θ = Máximo ângulo lateral de cada engate
β = Ângulo horizontal entre as linhas de centro
Condição: No caso da equação 1 resultar em um ângulo de contorno horizontal que exceda os limites da Tabela 2, aplicar as fórmulas da Equação 2, a qual leva em consideração uma análise geométrica mais aprofundada pois verifica o deslocamento lateral não apenas do conjunto mas de cada um dos engates envolvidos. Para isso, cada condição de giro é verificada, gerando um novo valor de ângulo a ser checado, agora com os vaçores individuais mostrados na Tabela 1.
SITUAÇÃO 2: Raio mínimo determinado pelo ângulo de cada um dos engates relativamente à linha de centro do vagão.
Fórmulas:
R = (B2 + L1)² – (D2)² – E / 2E Equação 2
E = L2 sen θ2 + L1 sen (θ2 + α) +X1 = X2 Equação 2.1
X1 = Y1 (D1 = B1 – L1) / (D1 + B1) Equação 2.2
X2 = Y2 (D2 + B2 + L1) / (D2 + B2) Equação 2.3
Y = (0,625(B / D) + 0,625) / 12 Equação 2.4
β = Arcsen (B2 + L1 / R + E) Equação 2.5
θ1 = θ2 + α – β Equação 2.6
Conhecidas estas situações de inscrição, nosso objetivo agora será o de exemplificar a aplicação destes conceitos na determinação do raio mínimo, o que será feito no proximo post.
Nossa sugestão, é que antes de iniciar a leitura e os cálculos da próxima publicação, se busque entender bem as figuras geométricas dos vagões em curva. Isto facilitará bastante a compreensão!!
Em resumo, inicie sempre pela SITUAÇÃO 1 e verifique o ângulo de contorno calculados para os dois engates acoplados. caso o limite deste ãngulo seja ultrapassado, faça nova verificação pela SITUAÇÃO 2 para verificar se o ângulo de giro lateral individual do vagão que está na tangente foi ultrapassado. caso seteja dentro, o valor de raio mínimo deve ser separado para comparação com os demais valores calculados para que se encontre o Raio Mínimo geral, o qual será o maior de todos os valores encontrados.
Caso a SITUAÇÃO 2 esteja fora dos limites, retornoe ao projeto do vagão e modifique as dimensões entre faces de tração e entre truques, fazendo novas verificações até que o equilíbrio seja encontrado.

