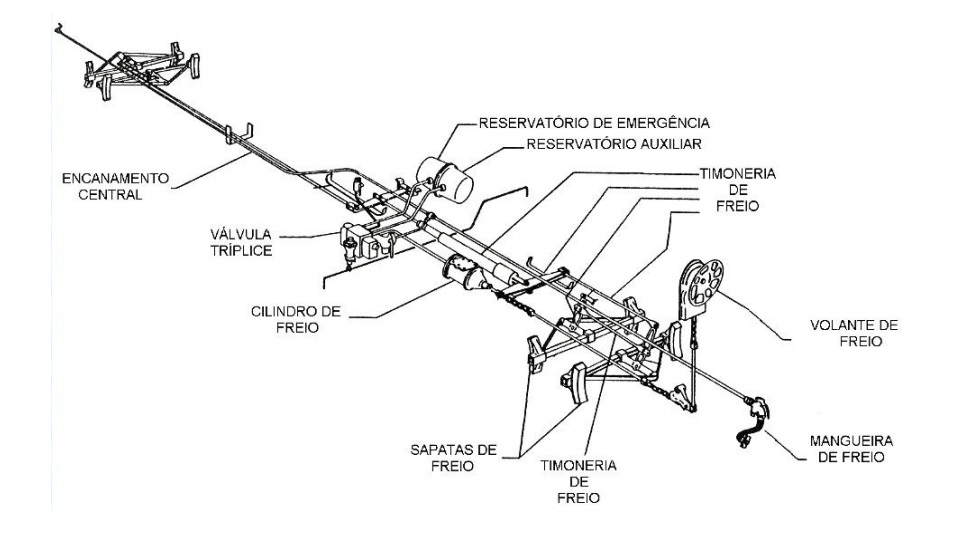
Concluídas as Partes 1 e 2 do nosso Projeto Básico de Timonerias de Freio, vamos agora nos dedicar a como dimensionar as peças que compôem o sistema. Nesta Parte 3, vamos definir as espessuras das alavancas, tirantes de tração, garfos de ligação, pinos e outros usados no vagão. Como comentários importantes, antes de iniciarmos o trabalho, podemos destacar:
A- As alavancas de freio podem ser fabricadas de chapas de aço recortadas em operação de oxi-corte ou forjadas. Porém, a opção forjada é regularmente usada nas alavancas dos truques porque estas já possuem uma dimensão padronizada nas ferrovias. Nelas, o tamanho e a furação são conhecidos e como estudamos, precisam ser mantidos para que nas operações de manutenção as equipes possam retirar um truque avariado e trocá-lo por outro, sem prejuízos aos limites de frenagem que calculamos na Parte 2, liberando o vagão ao tráfego no menor tempo possível.
B- O cálculo básico a ser usado nas alavancas de freio é a verificação quanto ao seu empeno em função do comprimento de sua furação, ou seja, verifica-se o momento aplicado na maior distância em relação ao seu centro. Caso o momento tenha a tendência de gerar uma deformação na alavanca a espessura deve ser aumentada. Assim, as forças de tração que já calculamos e que chegam pelos tirantes às alavancas, serão verificadas em relação ao momento gerado para definirmos a espessura de cada uma delas.
C- Para os tirantes, verificaremos a espessura da barra redonda que será usada. Quanto maior a força de tração que passa pelo tirante, maior será o diâmetro da barra de aço empregada. Sempre iremos considerar a tração como força básica de dimensionamento dos tirantes, com excessão da barra de compressão dos truques pois esta especialmente trabalha de forma inversa dos tirantes da timoneria.
D- Os garfos aplicados nas extremidades dos tirantes poderão também ser produzidos em chapa de aço recortada e dobrada, provida de furação onde serão instaladas buchas de desgaste em função do atrito com os pinos de conexão do freio ao longo do sistema. Importante será checar o movimento máximo da alavanca na qual o garfo estiver conectado para que não ocorra o “enforcamento” da alavanca. Isto significa que o tamanho do garfo pode ser pouco e a alavanca bater no fundo, impedindo a ação de frenagem. Na definição numérica do componente, este aspecto será mais explorado.
E- Os pinos de freio também serão definidos por barras redondas cortadas e usinadas para que estas peças tenham uma cabeça limitante adequada a manter os pinos sempre em posição. Outro aspecto importante dos pinos de freio será o tratamento térmico aplicado por cementação, aumentando sua resistência superficial ao desgaste. Lembremos que como foi dito na Parte 2, quanto mais folgas forem permitidas nas conexões menor será o rendimento da timoneria. Desta forma, realizando o tratamento térmico dos pinos, aumentaremos a vida útil do componente, mantendo a mesma perda inicial estimada.
Vamos repetir na Figura 1 abaixo, como ficou nossa timoneria hipotética após concluído o trabalho que realizamos na Parte 2,
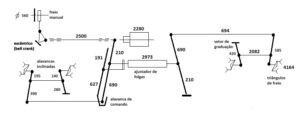
Figura 1 – Esquema da timoneria com indicação das força atuantes
Antes de iniciarmos o trabalho de dimensionamento, perguntamos: Qual poderia ser o coeficiente de segurança a aplicar no cálculo dos componentes? Como estabelecer um valor que nos garanta contra surpresas que poderiam ocorrer?
Exatamente para prevenir estas perguntas é que usaremos um procedimento previsto pela genialidade de Westinghouse: A aplicação de emergência!!!
VAMOS PENSAR UM POUCO!!!!
Sabemos que durante as aplicações de freio normais de operação, usadas para controle de velocidade dos trens ou para pará-los, o sistema utiliza apenas a porção de serviço do reservatório de ar. Quando por algum problema a emergência é acionada, todo o ar comprimido existente nos dois compartimentos do reservatório é usado, proporcionando uma pressão de equalização cerca de 20% maior. Esta informação foi confirmada em testes reais nas ferrovias com strain gages introduzidos no lugar das sapatas de freio para medir as forças reais nas rodas e pela inclusão de um manômetro ligado ao cilindro de freio.
Considerando que os vagões de um trem estejam todos equipados com válvulas do tipo ABDX, reservatório padrão com 41 litros de volume na porção de serviço e 57 litros na porção de emergência, cilindro de diâmetro de 10″ e um curso correspondente a 8″, a pressão de equalização será estabilizada por volta de 77 psi, ou seja 20% acima dos 64 psi de estabilização de uma aplicação normal. Esta indicação também pode ser comprovada no livro Engineering and Design Railway Brake Systems, da Air Brake Association – ABA, orgão que serve de base à normalização de freio da Association of American Railroads – AAR.
Como nossos trens seguem integralmente as condições prescritas nas normas AAR, estes valores serão aplicados diretamente em nossa operação.
Definida esta pressão de equalização nos cilindros em aplicação de emergência, vamos checar o valor de força baseados nas contas que fizemos na Parte 2 deste trabalho,
P = F / A e como
A = ¶ x d² / 4 Como o cilindro tem 10″ (254mm) de diâmetro, teremos A = ¶ x (254)² / 4
A = 3,1415 x (254)² / 4 o que nos dá A = 50.670,74 mm² (área interna do cilindro onde o ar comprimido atua)
Para conhecermos a força feita pela emergência, vamos usar o valor de 77 psi convertido em 0,054 kgf/mm² para encontrar
F = P x A …. F = 0,054 x 50.670,74 …. F = 2.736,22 kgf
Como a área interna do cilindro é constante, variando a pressão, variaremos de forma direta a força aplicada nas alavancas da timoneria. Para comprovar, dividindo o valor em emergência de 2.736,22 kgf por 2.280 kgf, oriundo da aplicação normal, encontraremos extamante os 20% de variação para mais que vimos na pressão de equalização do sistema. Este será o valor que usaremos para dimensionar os componentes de nossa timoneria de freio hipotética e para facilitar nossas contas, doravante consideraremos apenas o valor arredondado para 2.736 kgf.
Definido o valor de 20% a mais de força no cilindro de freio, usaremos a mesma relação para amplificar as forças que passam pelas alavancas e tirantes. Assim, vamos multiplicar cada força pelo fator de 1.2 para obter as forças nos componentes (ver valores no esquema da Figura 1 acima e Parte 2 deste trabalho)
F0 = 2.736,22 kgf = 2.736 kgf
F1 = 3.567,6 kgf = 3.568 kgf
F2 = 832,8 kgf = 833 kgf
F3 = 2.498,4 kgf = 2.498 kgf
F4 = 4.996,8 kgf = 4.997 kgf
Lembramos aqui que o valor representado por F4 é aquele que chega a um dos triângulos de freio, não sendo aqui diretamente considerado para o dimensionamento das peças da timoneria. Posteriormente, usaremos este valor para verificar mais à frente se o incremento de 20% nas forças de frenagem não influenciará no travamento das rodas. Como apresentamos, não podemos permitir que em caso de uma aplicação de emergência as rodas travem, deslizem e criem calos. Os vagões SEMPRE precisam ser freiados e parar com suas rodas girando, mesmo na condição mais crítica que é sob a aplicação de emergência.
Vamos então tecer alguns comentários à respeito da forma de dimensionamento dos componentes das timonerias, de acordo com as recomendações da ABA;
A- A resistência de todos os elementos das timonerias está baseada no trabalho em regime elástico do material no qual são fabricados. Isto significa que haverá uma deformação interna quando da aplicação das forças mas que tal deformação deverá desaparecer quando a força cessar;
B- Sempre devemos considerar um pequeno acréscimo da espessura ou seção resistente para compensar efeitos devidos ao desgaste por atrito ou por oxidação;
C- A experiência no ambiente ferroviário tem mostrado que as peças de uma timoneria devem suportar no máximo 2/3 da tensão de escoamento do material no qual foram construídas;
Trabalhando com cada componente segundo suas características funcionais e dimensionais, destacaremos a seguir como definí-los:
1- ALAVANCAS
As alavancas são os componentes mais conhecidos do sistema de timoneria e sempre que houver uma aplicação de freio, elas terão esforços ligados em suas extremidades pela atuação dos tirantes, gerando um movimento, que cessará quando todo o conjunto estiver em equilíbrio.
Devemos sempre observar o valor das forças atuantes e a distância de tais forças até o ponto da furação central na alavanca para encontrar o maior momento sobre a peça. Se tudo estiver corretamente dimensionado, as alavancas não se deformarão. Portanto, elas devem ter uma seção transversal suficientemente resistente para que a solicitação não ultrapasse a tensão de escoamento do material. Caso este limite seja atingido ou excedido, a alavanca se deformará de forma permanente. Como acontece na maioria dos componentes do sistema de freio, as alavancas deverão possuir uma boa resistência à fadiga, já que as cargas são continuamente aplicadas e aliviadas durante a operação do vagão.
Academicamente falando, poderíamos descrever o método de cálculo tradicional, o qual leva em consideração o momento gerado pela força do tirante multiplicada pela distância ao centro de furação da alavanca, em relação à tensão e ao momento de inércia da seção da alavanca, dividido pela distância da fibra externa ao eixo neutro da peça. Porém, para facilitar nosso trabalho a ABA (Air Brake Association) criou uma tabela resumo que relaciona o momento encontrado na alavanca com as espessuras mais comuns de chapas laminadas. Desta forma, nos basta calcular o valor do momento e buscar na tabela a largura da alavanca em função da espessura que usaremos na sua fabricação.
Para aqueles que quiserem conferir como a tabela que mostraremos a seguir foi criada, indicamos o livro da ABA mencionado acima, que é amplamente utilizado pelos projetistas de freio e de vagões que circulam sob as condições técnicas dos trens no ambiente da AAR.
Vamos então ver a Tabela de Alavancas:
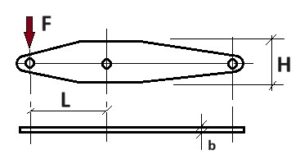
LARGURA (H) MOMENTO F x L (kgf x mm) PARA VÁRIAS ESPESSURAS
VALORES b = 19mm (3/4″) b = 25,4mm (1″) b = 31,7mm (1.1/4″)
63,5mm (2.1/2″) 207.014 276.019 345.024
69,8mm (2.3/4″) 250.445 334.080 417.485
76,2mm (3″) 298.138 397.670 496.858
82,5mm (3.1/4″) 349.862 466.445 583.027
88,9mm (3.1/2″) 405.734 540.979 676.224
95,2mm (3.3/4″) 465.754 620.928 776.218
101,6mm (4″) 529.920 706.522 883.238
107,9mm (4.1/4″) 598.234 797.645 997.056
114,3mm (4.1/2″) 670.694 894.298 1.117.786
120,6mm (4.3/4″) 747.302 996.365 1.245.312
127,0mm (5″) 828.058 1.104.192 1.380.096
133,4mm (5.1/4″) 912.845 1.217.664 1.521.792
139,7mm (5.1/2″) 1.001.434 1.337.472 1.670.400
146,1mm (5.3/4″) 1.094.976 1.460.736 1.824.768
152,4mm (6″) 1.193.472 1.590.912 1.988.352
Apresentada a tabela para definição das alavancas, vamos então usá-la para definir a espessura e a largura das peças que fazem parte de nossa timonera em função das forças atuantes na condição extrema de aplicação de emergência.
1.1- Alavancas principais
Nossa timoneria tem configuração tal que as alavancas principais do sistema são a alavanca ligada no cilindro de freio e que ao mesmo tempo recebe o tirante do freio manual e a alavanca do ponto fixo que transmite a força para o lado oposto. Para que se mantenha o importante equilíbrio, ambas as alavancas devem ser iguais dimensionalmente. Então, vamos avaliar para fechar a alavanca do cilindro, qual a força mais alta que chega na sua extremidade:
Força exercida pelo cilindro F0 = 2.736 kgf
Força do freio manual Fm = 2.500 kgf
Vamos então calcular a largura das alavancas principais usando a força do cilindro na condição de emergência, que é a maior das duas condições, definindo uma espessura de 25,4mm (1″) que é considerado um valor bom em função de resistência para um aço tipo ASTM A-36,
M = 2.736 kgf x 210mm = 574.560 kgf x mm
Este é o valor que deve ser procurado na tabela dimensional usando a coluna de espessura de 25,4mm, para encontrar uma largura de 95,2mm. Porém, como nossa timoneria possui alavancas com relativa diferença de distância de furação ao centro, vale a pena checar o momento do lado oposto para sabermos se não teremos surpresas. Então,
M = 833 kgf x 690mm = 574.770 kgf x mm
O que este resultado nos mostra? Mostra que o sistema se encontra em equilíbrio pois os momentos se equivalem!!
Em resumo, ambas as alavancas terão 95,2mm de largura com espessura de 25,4mm.
Caso o projetista queira ser conservador, poderá arredondar o valor da largura de 95,2mm para 96mm ou 100mm. OK?
Nota: Devido à simplicidade da timoneria que estamos estudando, não precisaremos definir as alavancas dos truques pois estas, como citamos, são padronizadas pelas ferrovias.
2- TIRANTES
Os tirantes de freio são sempre formados por barras de seção circular em aço SAE 1020. Este aço não é um aço de alta resistência mas pelas experiências realizadas ao longo do tempo e pelos cálculos realizados, é um mínimo aceitável para a fabricação dos tirantes de freio. Como os tirantes trabalham apenas à tração, como já dissemos, ficou definido pela ABA e aceito pela AAR a espessura mínima de 19mm (3/4″), crescendo conforme a tabela abaixo,
Força em kgf Diâmetro em mm
3.000 19,0 (3/4″)
4.100 22,2 (7/8″)
5.352 25,4 (1″)
6.760 28,6 (1.1/8″)
8.350 31,7 (1.1/4″)
10.115 34,9 (1.3/8″)
12.020 38,1 (1.1/2″)
14.100 41,3 (1.5/8″)
16.330 44,4 (1.3/4″)
18.780 47,6 (1.7/8″)
21.365 50,8 (2″)
Usando agora esta tabela e comparando com o quadro de forças de tração atuantes nos tirantes com os diâmetros listados, poderemos definir as barras que serão aplicadas na fabricação de cada componente
Tirante 1: neste ponto da timoneria está montado o ajustador de folgas que será estudado à parte
Tirante 2: são os dois tirantes ligados às alavancas dos truques com força F2 = 833 kgf. Usaremos o mínimo de 19,0mm (3/4″).
Tirante 3: não será definido pois neste ponto está a barra de compressão, a qual trabalha de forma oposta aos demais tirantes.
Tirante do freio manual: força de 2.500 kgf. Usaremos também o mínimo de 19,0mm (3/4″).
3- PINOS E GARFOS
Para fecharmos o dimensionamento dos componentes da timoneria, vamos então checar como definir os pinos e os garfos que ficam montados nas extremidades dos tirantes. Para estes dois itens, a ABA também preparou uma tabela dimensional de correção com as forças atuantes. Os pinos na verdade sofrem um tipo de cizalhamento duplo aplicado pelas duas seções do garfo e a seção da alavanca.
Pelas definições da ABA e da AAR, o mínimo diâmetro de pino deve ser de 27,8mm (1.3/32″), o que representa um valor 0,8mm (1/32″) menor que o diâmetro do furo onde ele será montado. Todos os pinos devem ser fabricados partindo de barras de aço usinadas e tratadas termicamente pelo método de cementação. Para os furos onde forem usadas buchas metálicas, os diâmetros dos furos dos garfos e das alavancas, devem ser preparados para recebê-las de forma que o diâmetro interno da bucha tenha o valor do pino acrescido da folga de 0,8mm.

Vamos então analisar os valores da tabela de correlação, os quais serão usados para a dimensão dos pinos e garfos de nossa timoneria
PINOS GARFOS
Máxima carga P (kgf) Mínimo diâmetro D (mm) Espessura t (mm) Valores de F (mm)
8.530 27,8 (1.3/32″) 25,4 (1″) 17,5 (11/16″)
10.570 31,0 (1.7/32″) 25,4 (1″) 20,6 (13/16″)
12.882 34,1 (1.11/32″) 25,4 (1″) 23,8 (1516″)
15.377 37,3 (1.15/32″) 25,4 (1″) 30,2 (1.3/16″)
18.100 40,5 (1.19/32″) 25,4 (1″) 34,9 (1.3/8″)
21.050 43,7 (1.23/32″) 25,4 (1″) 39,7 (1.9/16″)
Já verificamos acima que todas as alavancas terão 19mm de espessura e observamos que as forças ficarão abaixo dos 3.000 kgf. Logo, os garfos terão todos as seguintes dimensões nominais:
D = 27,8mm F = 17,5mm E =20,5mm G = 27,0mm H = 62,8mm
O projetista de freio poderá arredondar os valores conforme sua conveniência , lembrando que o comprimento do garfo dependerá do curso de giro da alavanca dentro do trabalho da timoneria para que o sistema não fique “enforcado” quando o ajustador de folgas estiver totalmente encurtado para acertar o desgaste das sapatas de freio.
Fechamos então a Parte 3 do nosso Projeto Básico de Timonerias de Freio, deixando a conclusão para a Parte 4 que será dedicada a algumas dicas sobre o correto posicionamento inicial do ajustador de folgas e das alavancas. Abraços e até la!!